金沢大学理工研究域数物科学系の川上裕准教授と自然科学研究科数物科学専攻博士前期課程修了生の渡邉元嗣は、これまで1種類しか見つかっていなかった、ガウス写像^（※1）の完全分岐値数が2.5の有限全曲率完備極小曲面の新しい例を発見しました。そして、3次元および4次元ユークリッド空間内の種数0の場合の有限全曲率完備極小曲面のガウス写像の値分布論的性質を明らかにしました。
　極小曲面とは、平均曲率が恒等的に0となる曲面のことです。空間内に閉曲線が与えられたときに、その曲線を境界に持ち、表面積が最小となる曲面は極小曲面となります。また、石鹸膜は表面張力によって面積が最小となるような曲面を形成します。このような背景から、極小曲面は石鹸膜の数学的モデル（図1）として現在でも活発に研究されています。

^{図1：立方体を境界にもつ石鹸膜}

　極小曲面論の研究における重要な問題の一つとして「完備極小曲面のガウス写像の除外値問題」があります。これは3次元ユークリッド空間内の平面でない完備極小曲面のガウス写像の除外値数の上限を求める問題で、1988年に藤本坦孝金沢大学名誉教授により最良の上限は4（図2）であることが示されています。藤本先生はこの業績で1988年に日本数学会幾何学賞を受賞しています。

^{図2：ガウス写像の除外値数が4の完備極小曲面の例（シャークの曲面）}

　一方、有限全曲率完備極小曲面のガウス写像については、1964年にオッサーマンにより除外値数は高々3であることが示されましたが、除外値数が3の曲面は現在も見つかっていません。除外値数が2の曲面はカテノイド（懸垂面）（図3）など存在が知られているので、有限全曲率完備極小曲面のガウス写像の除外値数の上限が2か3かのいずれかになり、それを問うのが『オッサーマン問題』と呼ばれる問題です。この問題の最終的な答えは現在でもわかっておらず、様々な観点から研究が進められています。

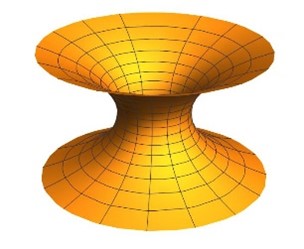^{図3：カテノイド（懸垂面）}

　もし除外値数の上限が2であれば、値分布論的観点から除外値数の拡張にあたる「完全分岐値数（欠除指数）」の上限も2であろうと予想されていましたが、その予想を覆す、ガウス写像の完全分岐値数が2.5 (=5/2)となる有限全曲率完備極小曲面の例（宮岡-佐藤の極小曲面）が2006年に発見されました。
　ガウス写像の完全分岐値数が2.5となる有限全曲率完備極小曲面の非自明な例はこれまでこの1種類しか見つかっていなかったのですが、今回の研究で渡邉元嗣が新しい非自明な例（図4）を発見しました。

^{図4：渡邉が発見した有限全曲率完備極小曲面（図は藤森祥一氏（広島大）による）}

　さらに、川上裕と渡邉元嗣との共同研究で、3次元および4次元ユークリッド空間内の種数0の場合の有限全曲率完備極小曲面のガウス写像の除外値数と完全分岐値数の評価と、それらの最良性を示す新しい例を得ることができました。
　本研究成果は、2024年6月25日に国際誌『The Journal of Geometric Analysis』にオンライン掲載されました。なお、本論文は金沢大学の支援を受けてオープンアクセスにしています。　　　
　本研究は、日本学術振興会科学研究費助成事業（19K03463・23K03086）の支援を受けて実施されました。

【用語解説】

※1　ガウス写像
曲面の単位法ベクトル場を、曲面から2次元単位球面への写像と見なしたものをその曲面のガウス写像といいます。日常的なものに例えると、ガウス写像は、海に船を浮かべたときに、その船に立てた棒であると考えることができます。海が穏やかなときに棒はあまり動かず、海が荒れているときに棒は激しく動きます。このようにガウス写像の挙動を調べることで曲面の曲がり具合を表すことができます。ガウス写像の除外値の数が少ないほど、その曲面は非常に曲がっていることが分かります。

 

The Journal of Geometric Analysis

• 研究者情報：川上　裕